【評価指標】ROC 曲線と AUC についてわかりやすく解説してみた

この記事はこんな方にオススメです

機械学習モデルの精度の評価方法について理解したい方
ROC 曲線、AUC の用語は知っているが深く理解できていない方

こんにちは、機械学習講師の竹内です。皆さんは機械学習で分類モデルを作成した際、モデルの精度をどのように評価すべきかご存知でしょうか。

モデルを評価する際に使用されるものを評価指標と呼び、分類モデルの場合は正解率 (Accuracy) や再現率 (Recall) 等、様々な評価指標があります。

今回は分類問題でよく使用される評価指標である ROC 曲線と AUC を紹介します。ROC 曲線とはなにかから具体的な計算方法までお伝えします。

補足

分類問題は機械学習の教師あり学習のタスクの 1 つです。分類問題について復習したい方は機械学習実践（教師あり学習：分類）も参考にしてみてください！

DX を推進する AI ・データサイエンス人材育成コース

プログラミング未経験から、AI やデータサイエンスを学ぶことのできる 6 ヶ月間のコースです。転職実績も豊富で、自走できる AI人材を多く輩出しています。

説明会はこちらから

真陽性率 (TPR) と偽陽性率 (FPR)
ROC 曲線とは
AUC とは
最後に：定義のまとめ
こちらの記事もオススメ
まずは無料で学びたい方・最速で学びたい方へ
- まずは無料で学びたい方： Python&機械学習入門コースがおすすめ
- 最速で学びたい方：キカガクの長期コースがおすすめ

真陽性率 (TPR) と偽陽性率 (FPR)

ROC 曲線の概要の前提知識として真陽性率 (TPR : True Positive Rate) と偽陽性率 (FPR : False Positive Rate) についてお伝えします。

TPR とは全ての Positive のうち、実際に Positive だったものを正しく Positive と判定できた割合です。そして FPR は全ての Negative のうち、実際には Negative だったが間違えて Positive と判定した割合です。ここで Positive と Negative の定義を行っていないため何を伝えたいのかわからないと思います。

そこでねじを生産する工場の具体例を用いて、TPR と FPR について理解を深めていきましょう。生産したねじが異常品か正常品かを分類する機械学習モデルを作成したとします。

このモデルを使用して 1000 個のねじを異常品、正常品に分類する作業を行いました。その結果以下のような分類を行いました。

上図の表を混同行列と呼びます。この時、正常品と異常品のそれぞれに Positive と Negative のラベルを付けます。今回は異常品を Positive、正常品を Negative とします。

補足

今回は異常品を Positive、正常品を Negative と設定しましたが、もちろん異常品を Negative、正常品を Positive と設定しても問題ありません。

このように設定するという厳密なルールはありませんが、一般的には検出したい方（今回であれば異常品はなるべく検知したいので異常品）を Positive に設定することが多いです。

この時、全異常品のうち、実際に異常品だったものを正しく異常品と判定できた割合（40%）が TPR、そして全正常品のうち、実際は正常品だったが間違えて異常品と判定した割合（約 5%）が FPR になります。計算すると以下になります。

最初にお伝えした定義を再掲しておきます。

TPR、FPR の定義

TPR とは全ての Positive のうち、実際に Postitive だったものを正しく Positive と判定できた割合です。
FPR は全ての Negative のうち、実際には Negative だったが間違えて Positive と判定した割合です。

上記の定義が理解できたのではないでしょうか。それではこの TPR と FPR を押さえた上で、ROC 曲線と AUC を理解していきましょう。

ROC 曲線とは

ROC 曲線とは以下の図のような曲線です。

各軸は TPR、FPR を表しており、Positive と Negative に分類する際の閾値を変更した際の TPR、FPR の値をプロットしています。こちらも定義だけではイメージが掴みにくいと思いますので、具体例を使用してお伝えします。

ROC 曲線の理解を深めるため今回も異常品検知の例（ねじを生産する工場）を使用します。正常品、異常品を分類するモデルを使用して 1000 個のねじの分類を行った結果、以下の表のようなデータが得られました。（異常品が Positive、正常品が Negative です。）

この結果をヒストグラムで表すと以下になりました。

実際に異常品だったものは赤色、実際に正常品だったものは青色で表しています。この時、Positive（異常品）である確率が 0.5 以上かそれ未満で Positive と Negative を分類すると仮定すると以下の図になります。

上図で示すように正しく Positive と分類できているところと、間違って Positive と分類しているところがあります。それでは Positive（異常品）である確率が 0.8 以上かそれ未満で Positive と Negative を分類するように変更すると以下の図になります。

ここで、閾値を変更すると TPR と FPR の値が変わっていることがわかります。（閾値を 0.8 に設定した際は FPR=0 になっています。）ここで定義を再掲します。

ROC 曲線の定義

Positive と Negative に分類する際の閾値を変更した際の TPR、FPR の値をプロットしています。

上記の定義を実際に行うと以下のようになります。

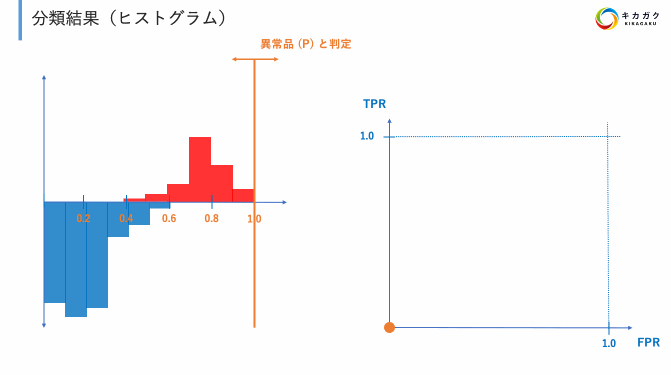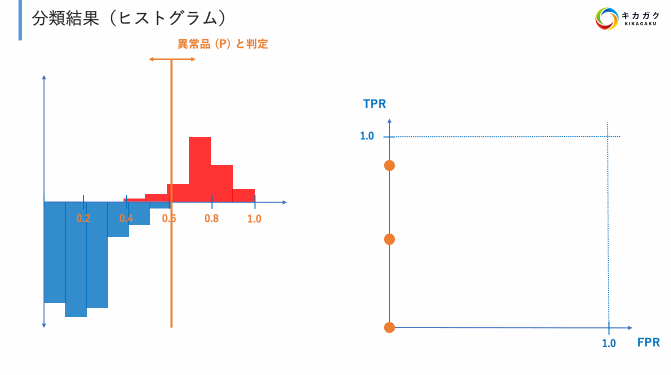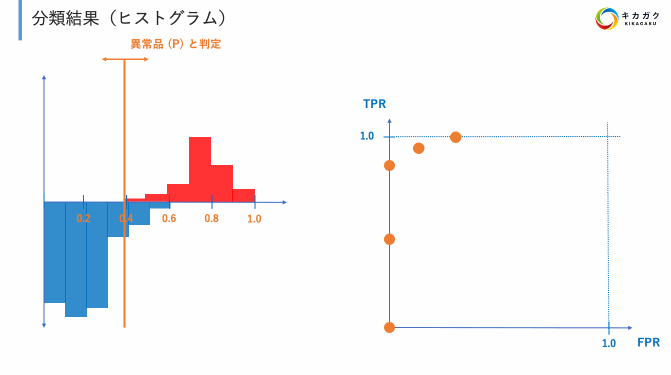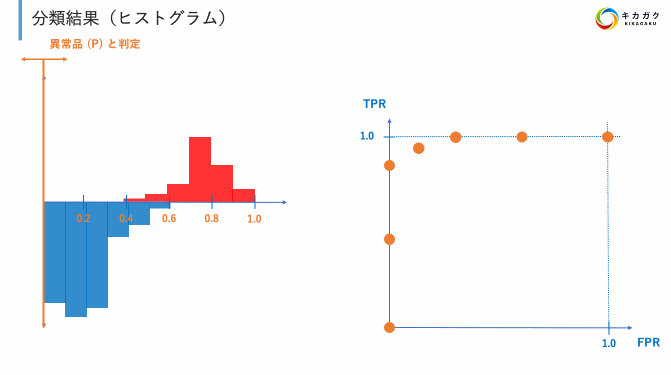
そしてプロットされた点を直線で結んだものが ROC 曲線です。

この ROC 曲線が理解できれば AUC は非常にわかりやすいです。

AUC とは

AUC は Area Under the Curve の略であり、ROC 曲線の下部分の面積のことです。

この AUC がなぜ分類モデルの評価として有効なのかを考えてみます。例えば以下のように分類できていたとします。

かなりきれいに分類できています。上図の結果を ROC 曲線で表すと以下のようになります。

この時の AUC は 1 になります。それでは以下のような分類の場合はどうでしょうか。

すべての確率に均等にサンプルが存在しているので適切な分類ができていません。上図の結果を ROC 曲線で表すと以下のようになります。

この時の AUC は 0.5 になります。つまり Positive と Negative をきれいに分類できていれば AUC は 1 に近づき、ランダムな分類をしていると AUC は 0.5 に近づくことがわかります。

このことから AUC が 1 に近いほど、優れた分類モデルであるといえます。

最後に：定義のまとめ

最後に本記事で紹介した用語とその定義をまとめておきます。

TPR : True Positive Rate

全ての Positive のうち、実際に Posititive だったものを正しく Positive と判定できた割合。

FPR : False Positive Rate

全ての Negative のうち、実際には Negative だったが間違えて Positive と判定した割合。

ROC 曲線

各軸が TPR、FPR を表し、Postitive と Negative に分類する際の
閾値を変更し、各閾値時の TPR、FPR をプロットしたグラフ。

AUC : Area Under the Curve

ROC 曲線と TPR=0、FPR=1 の直線で囲まれる部分の面積。

この他にも機械学習のモデルに使用される評価指標は様々ありますので、好評であれば他の指標もまとめていきたいと思います！

こちらの記事もオススメ

まずは無料で学びたい方・最速で学びたい方へ

まずは無料で学びたい方： Python&機械学習入門コースがおすすめ

AI・機械学習を学び始めるならまずはここから！経産省の Web サイトでも紹介されているわかりやすいと評判の Python&機械学習入門コースが無料で受けられます！
さらにステップアップした脱ブラックボックスコースや、IT パスポートをはじめとした資格取得を目指すコースもなんと無料です！

無料で学ぶ